C’est un drôle de vieux (jeu de) vie. Mais joueriez-vous à une version d’automate cellulaire ?
Le jeu de la vie de Conway est une forme de vie artificielle appelée automate cellulaire. Bien que les règles soient simples, les résultats peuvent être étonnants.
As-tu déjà vu La momie film de 1999 avec Brendan Frazer ? (J’ai aussi adoré Brendan dans son rôle dans Georges de la jungle à partir de 1997.) Il y a une partie dans le film où des milliers de scarabées – qui sont Dépeints comme étant d’anciens coléoptères mortels qui mangent des organes internes et externes – sortent du sol et commencent à dévorer tout le monde en vue. (Au cas où vous vous poseriez la question, les cinq organes externes sont considérés comme les yeux, les oreilles, le nez, la langue et la peau.)
Ces créatures sont animées, mais avez-vous déjà pensé à la façon dont cette animation a été réalisée ? Il faudrait un temps et des efforts ahurissants pour diriger individuellement les actions de chacun de ces insectes. L’astuce consiste d’abord à définir comment un scarabée individuel peut se déplacer et à mettre en place un ensemble de règles simples qui déterminent comment un scarabée peut réagir à tout objet et autre scarabée à proximité. Après cela, tout ce que vous avez à faire est de définir les chemins d’une poignée de « leaders scarabées », et le reste suivra.
Le premier exemple que j’ai vu de ce genre de chose était un programme de simulation de vie artificielle appelé Boids, développé par le gourou de l’infographie Craig Reynolds en 1986. objet ressemblant à un oiseau »). Par une étrange bizarrerie du destin, « boid » est aussi la façon dont les gens prononcent « oiseau » dans la métropole de New York.
Un bon résumé de ce concept est fourni par Wikipedia, qui nous dit que : « Comme avec la plupart des simulations de vie artificielle, Boids est un exemple de comportement émergent ; c’est-à-dire que la complexité des Boids résulte de l’interaction d’agents individuels (les Boids, dans ce cas) adhérant à un ensemble de règles simples. Les règles appliquées dans les mondes Boids les plus simples sont les suivantes : séparation (diriger pour éviter d’entasser les compagnons de troupeau locaux), alignement (diriger vers le cap moyen des compagnons de troupeau locaux) et cohésion (diriger pour se déplacer vers la position moyenne (centre de masse) de compagnons de troupeau locaux). Des règles plus complexes peuvent être ajoutées, telles que l’évitement d’obstacles et la recherche de but.
Juste pour vous donner une idée de ce dont je parle, jetez un œil à cette vidéo de 2007 montrant une volée de boids suivant une cible (une boule verte) et évitant un objet fixe (une sphère rouge). Bien sûr, des comportements similaires peuvent être appliqués aux bancs de poissons, comme on le voit dans cette simulation, ou aux scarabées dans les films d’horreur.
Une autre forme de vie artificielle est celle d’automate cellulaire (pluriel automates cellulaires, abréviation CA). Une CA implique un « univers » formé d’une grille de cellules, dont chacune peut être dans l’un d’un nombre fini d’états. L’état de chaque cellule est affecté par les conditions des autres cellules dans son voisinage local. Au début de la simulation, un état initial de « graine » est appliqué aux cellules, après quoi un petit nombre de règles sont utilisées pour passer d’une génération à la suivante.
Le concept CA a été initialement découvert dans les années 1940 par Stanislaw Ulam et John von Neumann. En même temps, ils étaient contemporains du Laboratoire national de Los Alamos. Pourtant, les choses n’ont décollé qu’en 1970, lorsque le mathématicien britannique John Horton Conway a inventé son CA appelé Game of Life (GOL).
Conway était en quelque sorte un « personnage » décrit comme étant « Archimède, Mick Jagger, Salvador Dali et Richard Feynman tous réunis en un seul ». Dans son incarnation originale en deux dimensions (2D), l’univers dans lequel se déroule le GOL est une grille infinie de cellules carrées (plus récemment, certaines personnes ont expérimenté des univers en trois dimensions (3D) formés à partir d’un réseau infini de cellules cubiques ).
Chaque cellule du GOL peut être dans l’un des deux états possibles : « vivant » ou « mort. » De plus, chaque cellule interagit avec ses huit « voisins », qui sont les cellules adjacentes horizontalement, verticalement ou en diagonale. Ainsi, nous commençons par semer l’univers avec un motif, qui pourrait impliquer une ou plusieurs combinaisons spécifiques de cellules, ou il pourrait être généré de manière aléatoire. Nous laissons ensuite la simulation évoluer d’une génération à l’autre en utilisant l’ensemble de règles suivant :
- Toute cellule vivante avec moins de deux voisins vivants meurt, comme par sous-population.
- Toute cellule vivante avec deux ou trois voisins vivants vit jusqu’à la génération suivante.
- Toute cellule vivante avec plus de trois voisins vivants meurt, comme par surpopulation.
- Toute cellule morte avec exactement trois voisins vivants devient une cellule vivante, comme par reproduction.
Les naissances et les décès se produisent simultanément, et chaque nouvelle génération est une pure fonction de la génération précédente. Ainsi, bien que ces règles puissent paraître simples à la lecture, il peut falloir une certaine gymnastique mentale pour les appliquer. Considérez l’illustration suivante, par exemple :
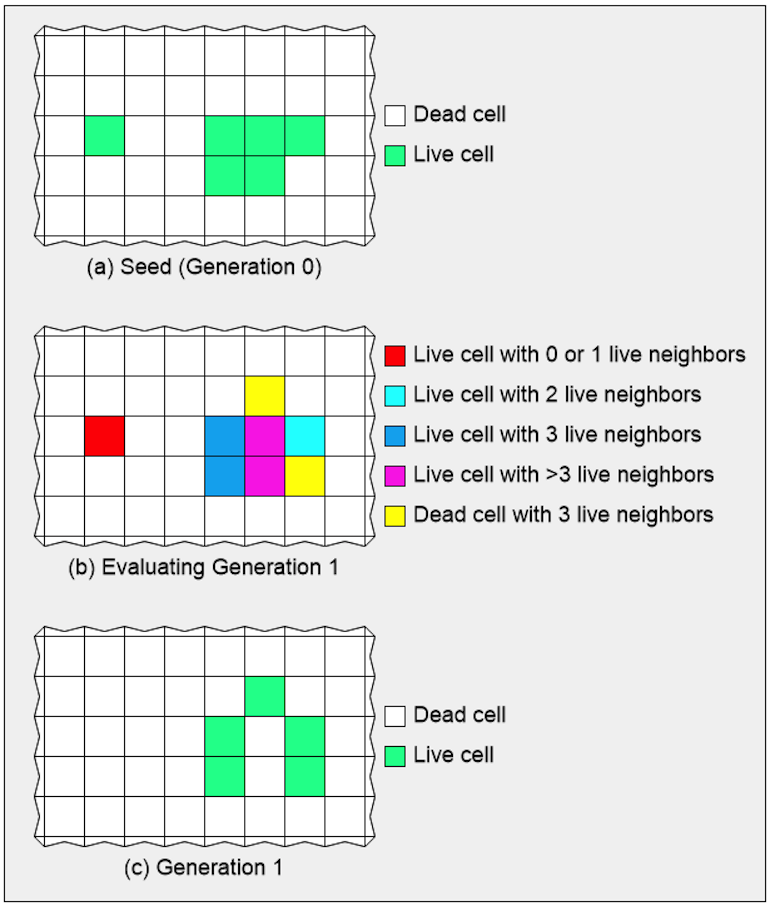
Un petit groupe de cellules dans un univers GOL.
Nous commençons par notre génération de semences, que nous pouvons appeler la « génération 0 ». Nous considérons ensuite chaque cellule dans le contexte de ses voisines. Pour chaque cellule, il y a deux choix. Si une cellule est actuellement vivante, elle restera en vie ou mourra dans la génération suivante. De même, si une cellule est maintenant morte, elle restera morte ou reprendra vie dans la génération suivante.
Vous devez admettre que déterminer ce qui va se passer n’est pas trop facile si vous le faites à la main. Mais, bien sûr, c’est facile de presser le citron si vous avez un ordinateur pour le faire pour vous. La chose étonnante pour moi est que Conway n’avait pas accès à l’ordinateur lorsqu’il a inventé son GOL. Au lieu de cela, lui et ses collègues ont passé d’innombrables heures à jouer avec des cailloux sur un plateau GO pour déterminer l’ensemble de règles optimal avec lequel ils se sont retrouvés.
Ce qui est passionnant, c’est que, bien que les règles GOL elles-mêmes soient simples, le comportement qui en résulte peut être très complexe. Par exemple, certains modèles sont appelés « natures mortes » car ils restent statiques d’une génération à l’autre, à moins qu’ils ne soient perturbés par l’empiètement des cellules. Le niveau suivant est celui des « oscillateurs », qui reviennent à leur état initial après un nombre fini de générations. Ensuite, nous avons des «vaisseaux spatiaux», qui se traduisent (se déplacent) à travers la grille (le plus simple d’entre eux est le «planeur Gosper», qui a été découvert par Bill Gosper en 1970). Et nous avons aussi des « pistolets », qui sont des motifs qui ont une partie centrale qui se répète périodiquement, comme un oscillateur, et qui émettent aussi parfois des vaisseaux spatiaux. Tout ce que je peux dire, c’est qu’une simulation GOL complète est quelque chose à voir (recherchez « Game of Life » sur YouTube pour voir quelques exemples notables).
La raison pour laquelle je m’attarde sur tout cela ici, c’est parce que j’ai décidé de mettre en œuvre mon propre GOL. Comme vous vous en souvenez peut-être dans les colonnes précédentes (voir Le tableau de balles de ping-pong brille et Ajoutez facilement la détection de mouvement et d’orientation pour améliorer vos projets), j’ai créé un réseau de balles de ping-pong 12×12, où chaque balle est équipée d’une LED tricolore. Comme j’avais déjà ce tableau à ma disposition, j’ai décidé de l’utiliser comme mécanisme d’affichage pour un simple GOL.
Bien sûr, un problème est que l’univers GOL est censé être infini, donc un tableau 12×12 de ventes est un peu court. La façon dont j’ai contourné cela était de rendre mon univers de tableau « courbe ». Nous pouvons imaginer notre univers comme étant enroulé dans un cylindre vertical de telle sorte que le côté droit s’enroule et rencontre le côté gauche, de sorte qu’un vaisseau spatial « sortant à droite de la scène » « réapparaîtra à gauche de la scène ». De même, et simultanément, nous pouvons imaginer notre univers comme étant enroulé dans un cylindre horizontal de telle sorte que le côté supérieur s’enroule et rencontre le côté inférieur, de sorte que tout ce qui « tombe du bas » réapparaîtra en haut.
La meilleure façon de visualiser cela est de le regarder en action. Comme le montre cette vidéo, nous commençons par charger le tableau avec une graine aléatoire, exécutons la simulation jusqu’à ce que toutes les cellules soient mortes, puis recommençons à zéro. Malheureusement, les deux premiers motifs aléatoires disparaissent assez rapidement. Cependant, la troisième graine aléatoire s’avère beaucoup plus intéressante.
Ce qui est amusant, c’est que lorsque j’ai construit à l’origine mon tableau 12×12, je n’avais aucune idée de tout ce que je finirais par faire avec. Maintenant, de nouvelles idées me viennent à l’esprit presque tous les jours. Par exemple, je pense à la construction d’un tableau plus grand (de la taille d’un mur) – je ne peux qu’imaginer à quoi ressemblerait un GOL là-dessus. Et toi? Avez-vous des pensées que vous voudriez partager à ce sujet ?